
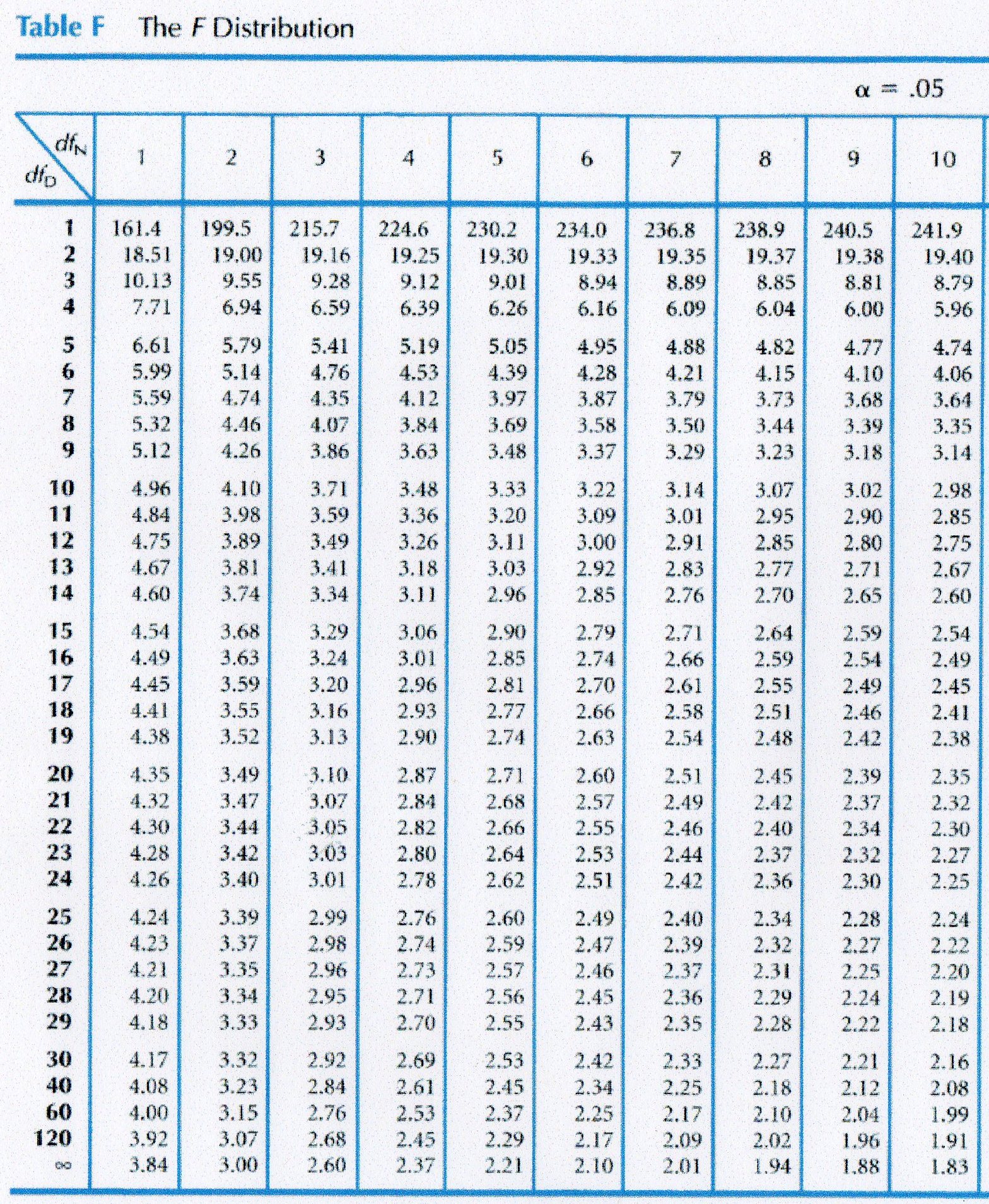
While portraying a F conveyance, the quantity of levels of opportunity related with the standard deviation in the numerator of the f measurement is constantly expressed first. The bend of the F conveyance relies upon the levels of opportunity, v1 and v2. The conveyance of all potential estimations of the f measurement is called a F dissemination, with v1 = n1 - 1 and v2 = n2 - 1 levels of opportunity. Note that levels of opportunity v1 = n1 - 1, and levels of opportunity v2 = n2 - 1. Where σ1 is the standard deviation of populace 1, s1 is the standard deviation of the example drawn from populace 1, σ2 is the standard deviation of populace 2, s2 is the standard deviation of the example drawn from populace 2, Χ21 is the chi-square measurement for the example drawn from populace 1, v1 is the levels of opportunity for Χ21, Χ22 is the chi-square measurement for the example drawn from populace 2, and v2 is the levels of opportunity for Χ22. The accompanying comparable conditions are ordinarily used to process a f measurement: The f measurement is the proportion of s12/σ12 and s22/σ22. Select an autonomous arbitrary example of size n2 from a typical populace, having a standard deviation equivalent to σ2. Select an arbitrary example of size n1 from a typical populace, having a standard deviation equivalent to σ1. Here are the means needed to register a f measurement: (We talk about the F dissemination in the following segment.) The f measurement, otherwise called an f esteem, is an arbitrary variable that has a F dispersion.
#Calculator f distribution how to#
In this exercise, we tell the best way to process an f measurement and how to discover probabilities related with explicit f measurement esteems. The F conveyance is the likelihood circulation related with the f measurement. There is lot of students who wants to solve their Equation really quick so but this will be really great tool for those students. Suppose if you will do it manually then it will take lot of time. magnetic force on straight current carrying wireį-Distribution calculator is a great tool to use that will help you solve your problem Really Quick.Rotational and periodic motion calculators Numerical Analysis - Numerical Differentiation Tools Improper fraction to mixed number calculator.Mixed number to Improper fraction calculator.Print 'a or b too large or given ITMAX too small for computing incomplete beta function. (Code translated from: Numerical Recipes in C.)"""ĭ = -(a+em)*(qab+em)*x/((qap+tem)*(a+tem)) """ contfractbeta() evaluates the continued fraction form of the incomplete Beta function incompbeta(). Return 1 - math.exp(lbeta) * contfractbeta(b, a, 1-x) / b
Return math.exp(lbeta) * contfractbeta(a, b, x) / a Lbeta = math.lgamma(a+b) - math.lgamma(a) - math.lgamma(b) + a * math.log(x) + b * math.log(1-x) (Code translated from: Numerical Recipes in C.)''' This function requires contfractbeta(a,b,x, ITMAX = 200) ''' incompbeta(a,b,x) evaluates incomplete beta function, here a, b > 0 and 0 <= x <= 1. Just in case the blog disappears, here the code: import math Here the result for some sample values, matching .sf: In : F, df1, df2 = 5, 20, 18
#Calculator f distribution code#
Using the code for I(x a, b) from this blog, which uses only math, the p-value is 1 - incompbeta(.5*df1. The CDF for the F-distribution (and hence the p-value) can be calculated with the regularized (incomplete) beta function I(x a, b), see, e.g., MathWorld.


 0 kommentar(er)
0 kommentar(er)
